Data science

Data science kan beskrivas som metoder som utvinner kunskap eller insikter från data, vare sig den är strukturerad (som statistik) eller ostrukturerad (som text).

60 år av kommunikationsforskning i en graf

Peter Dahlgren Leave a comment

En ny intressant studie publicerades med en analys av 149 meta-analyser. Jag plockade ut och laddade upp alla effektstorlekar på GitHub för den som vill analysera dem själv, och konstruerade graferna nedan.

I den första grafen ser du distributionen av effektstorlekarna. Medelvärdet är r = 0,21, vilket intressant nog är identiskt med socialpsykologi (se även effektstorlekar från socialpsykologi på GitHub som jag laddat upp).

Uppdelat på sex olika fält ser man exempelvis att det mesta är relativa låga effektstorlekar, men att exempelvis organisations- och gruppkommunikation åtminstone har lite större effekter.

Däremot återfinns de största effekterna under påverkan (Persuasion). Detta är dock sådant som handlar om sambandet mellan attityd och beteende, det vill säga vad vi tycker också tenderar att reflekteras i vad vi gör.

Data och källkod för att producera graferna (inklusive fler typer av grafer) finns på GitHub på länkarna ovan.

De snabbast växande orden i två miljoner nyhetsrubriker under tre år

Peter Dahlgren Leave a comment

Vilka ord har ökat och minskat i bruk bland drygt två miljoner nyhetsrubriker från 2014 till 2017? I den här analysen har jag tagit nyhetsrubriker som är insamlade från början av 2014 till och med juni 2017 för att se vilka ord som förekommit mest och vilka som har snabbast ökat i popularitet.

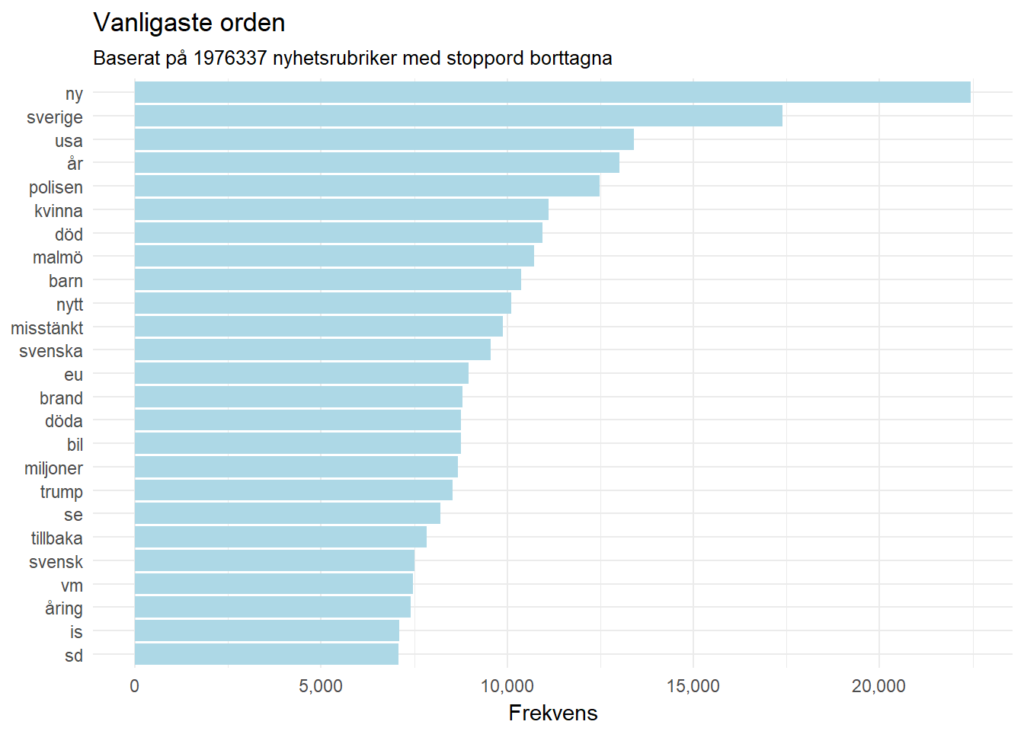
Vilka ord har ökat mest på kortast tid? Kanske inte så förvånande är Donald Trump väldigt omskriven, precis som på Twitter. Lika lite förvånande är det ett väldigt fokus på USA och Storbritannien.

Men intressant nog verkar också vanlig lokal nyhetsvärdering öka relativt mycket, apropå ”trafikolycka” och ”singelolycka”.

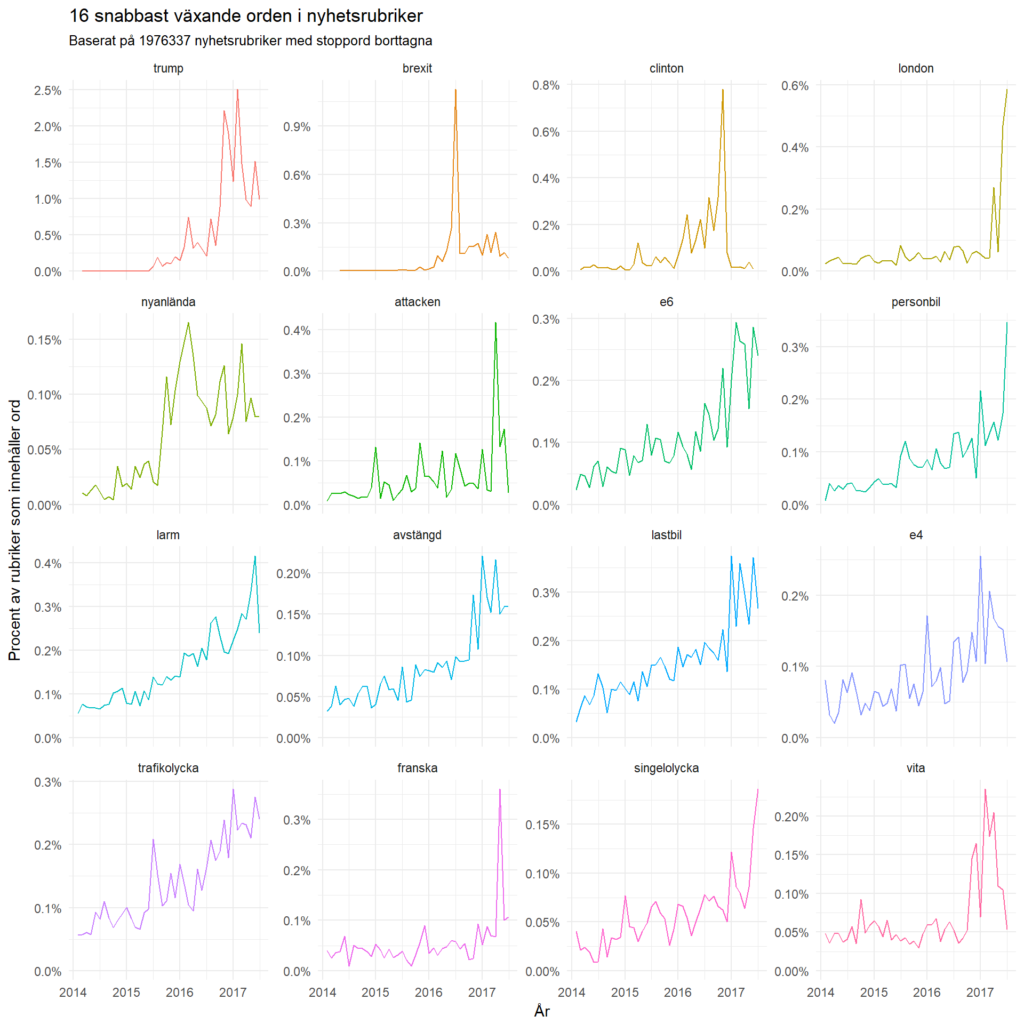
Se också de snabbast sjunkande orden.

Tittar man på de ord som ökade mest under 2015 så är det ”flyktingar”, vilket jag satt i relation till ”migrationer” respektive ”nyanlända”. Av grafen att döma verkar de svenska medierna nästan unisont börja skriva om flyktingar vid samma tillfälle, därav den vertikala ökningen av texter.

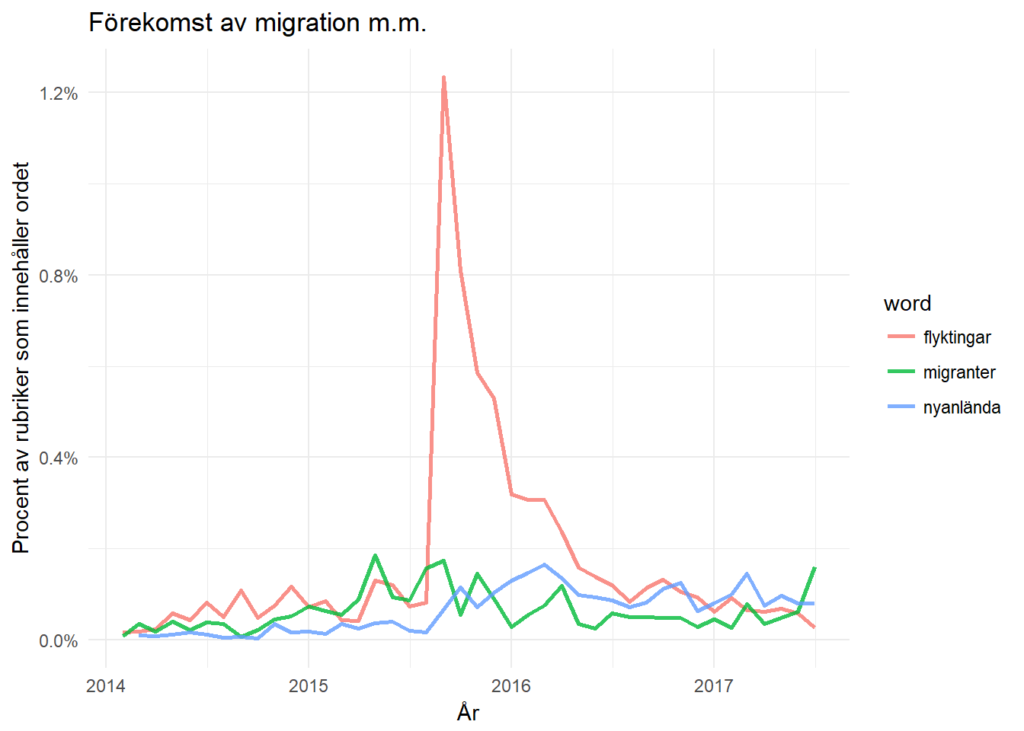
De här graferna har jag mest gjort för skojs skull, men jag tänker mig att denna typ av analyser kan vara en förhållandevis enkel början till att forska om agenda-sättning. Över lång tid ger de här analyserna väldigt intressant information jämfört med de korta nedslag som ofta görs i forskningen.

Mer intressant, tror jag, är att de också också kan användas för att identifiera var man bör starta sin undersökning (eftersom de är helt induktiva), snarare än att hipp som happ sätta upp sitt blöta finger i luften för att mäta vart vinden blåser.

Den fullständiga analysen har jag som vanligt lagt upp på GitHub där du hittar både källkod och länkar till datan som du kan ladda ned. Kom gärna med förslag på hur det kan göras annorlunda.

Fler analyser

Här är några andra analyser jag gjort i R med framför allt öppna data:

Big data i medieforskning

Att bara analysera rubriker går bra på en vanlig laptop. Det var inga svårigheter att ladda in en miljon rubriker i minnet. Vid två miljoner rubriker började datorn gå på knäna. R tog 11 gigabyte i anspråk för att köra unnest_tokens för att skapa en vektor på drygt 5,1 miljoner ord mappat till nyhetsrubrikerna.

Framöver behövs mer datorkraft för analyser av hela brödtexten, kanske med hjälp av Apache Spark som jag använt tidigare. Dock ska jag testa om bigmemory i R kan fungera eftersom den, vad jag förstår, genomför analysen på disken snarare än i minnet. Det går lite långsammare, men om man sysslar med forskning så är allt redan långsamt.

RMarkdown

Dokumenten i listan med länkarna ovan är gjorda med hjälp av RMarkdown, ett sätt att blanda källkod i valfritt språk, bilder, text och… tja, allt man kan tänka sig. Även om RMarkdown är skapat för språket R fungerar även andra språk och jag har exempelvis skrivit Python-kod i RMarkdown som jag använde som presentation under en lektion i web scraping. Det går med andra ord utmärkt att exportera till Powerpoint, Word, hemsidor eller PDF.

Det är ett behändigt sätt att paketera sina analyser. Steget från källkod till presentation blir minimalt, och det är också varför den brittiska regeringen valt att satsa på RMarkdown.

Jag tror detta kommer bli vanligare i framtiden. I stället för att presentera ett begränsat antal analyser på ett lika begränsat antal sidor så kan man dokumentera hela sin process för att låta andra upptäcka hur tankeprocessen har gått till, och även se resultat man kanske borde följa upp. Detta kan sedan bifogas till artikeln i ett appendix så att man kan se diagram och källkod tillsammans.

Frågan är vilken tidskrift som blir först med kräva att analyserna i Markdown bifogas till varje artikel? Stata 15 har ju också kommit ut med Markdown så R är ju knappast något krav längre.

Länkkarteller på #svpol

Peter Dahlgren Leave a comment

Okej, rubriken till trots handlar detta inte riktigt om länkkarteller. Det låter bara tufft att säga kartell.

Vad jag däremot har gjort är att återskapa Kate Starbirds metod från Information Wars: A Window into the Alternative Media Ecosystem som visar sajter som brukar länkas tillsammans på sociala medier när konspirationsteorier förs på tal.

Vilka länkar förekommer mest tillsammans? Det är frågan som bilden nedan svarar på. Men i stället för konspirationsteorier har jag valt att titta på #svpol generellt sedan november 2015. Och där dominerar traditionella massmedier. Det är huvudsakligen kvintetten Expressen, Aftonbladet, SVT, DN och SvD som förekommer mest tillsammans på #svpol, vilket tjockleken på linjerna och de röda bubblorna indikerar.

Jag använde algoritmen DrL för att skapa nätverket, som är force-directed, vilket i korthet innebär att domäner längre ifrån varandra har mindre med varandra att göra (färre länkar tillsammans). Därmed hamnar massmedierna i gröten i mitten eftersom de får flest länkar.

Läs mer

Se hela analysen av #svpol eller ladda ned källkoden i R om du vill göra samma sak själv.

Vad som varit populärt på Twitter under ett år

Peter Dahlgren Leave a comment

Trender är vad de sociala medierna som Twitter och Facebook själva kallar vad som är populärt just nu. Genom att undersöka dessa är det möjligt att se vad folk skriver och diskuterar.

Eftersom trender är offentliga för alla att se, är de sällan avbilder av vad människor skriver, tycker eller tänker eftersom trenderna också kan påverka vad människor väljer att skriva om. Det som är populärt kan därför bli ännu mer populärt (samma problem finns med opinionsundersökningar).

Här är exempelvis de tio vanligaste trenderna på Twitter under året, med antalet trender inom parentes:

  1. #ffse (1 662)
  2. #aktuellt (1 435)
  3. #lyrikfredag (1 374)
  4. #sthlmpol (1 218)
  5. United (1 042)
  6. Liverpool (1 027)
  7. Chelsea (1 001)
  8. Zlatan (983)
  9. Hovet (939)
  10. #GONINJAS (922)

Exakt hur Twitter avgör vad som är en trend är höjt i dunkel, men trender reflekterar dels vad som händer just nu snarare än vad som händer för dagen, och dels volymen av tweets. Med andra ord, ju fler tweets under en kort period, desto större chans att det blir en trend. Av det skälet valde jag att samla in trender varje timme, dygnet runt, under ett år.

Trender är personliga, men det är också möjligt att ange en plats för var man vill se trender. I det här fallet har jag valt Sverige som plats för att se vad som skrivs i Sverige under ett år.

Nedan ser du några diagram jag tagit fram för massmedier och politiska partier, som bygger på trender från mars 2016 till mars 2017.

Massmedier

Massmedierna har jag plockat fram genom att helt enkelt gå igenom ett stort antal av de mest förekommande trenderna och sedan lagt in dem i diagrammet.

SVT-programmen Aktuellt dominerar tillsammans med Opinion Live, men Expressen Live kommer inte långt efter. Det är de som har trendat flest gånger.

Politiska partier

När det gäller de politiska partierna visar diagrammet nedan hur ofta respektive partis namn har trendat. Räknat på detta sätt är det Moderaterna som har flest trender.

Du hittar hela analysen i form av en R Markdown notebook: Vad som trendat på Twitter under ett år. Data finns även fritt tillgänglig via GitHub.

Hur stor blir felmarginalen vid en viss urvalsstorlek?

Peter Dahlgren Leave a comment

Hur stor blir felmarginalen vid en viss urvalsstorlek? Denna enkla fråga tänkte jag besvara genom att måla upp en graf.

Felmarginaler är ett roligt ämne. I stället för att traggla med formler eller tabeller försöker jag göra så mycket som möjligt visuellt, i synnerhet när jag ska visa för andra vad det egentligen är som händer. Det brukar vara lättare att förstå om man kan se resultaten av det man gör, snarare än att försöka bygga en abstrakt modell i huvudet av vad som händer (vilket förvisso inte ska underskattas det heller).

Jag försöker också dra nytta av mina programmeringskunskaper och lära mig R bättre. Så varför inte göra ett litet skript som gör allt det manuella arbetet till något som kan återanvändas och presenteras grafiskt?

Här kommer därför en liten bild som visar felmarginalerna vid olika urvalsstorlekar. Det gör det förhoppningsvis lite lättare att förstå varför man använder ungefär 1 000 personer i olika former av opinionsundersökningar, snarare än 2 000 eller 3 000. Vinsten av att använda fler personer än tusen är ofta inte särskilt stor.

Jag har också medvetet valt ett alternativ med 50 % eftersom felmarginalen blir som störst då. Det beror på att det i formeln finns en kvadratisk funktion (p * (1 - p)). Ju närmare mitten i intervallet 0 och 100 %, desto större blir helt enkelt osäkerheten.

Hur urvalsstorleken påverkar felmarginalen

Som du ser i koden nedan så förutsätter jag 95 % konfidensintervall om man inte anger något annat. Man måste dock skriva z-värdet, så därför bifogar jag en liten lathund över dessa. Och som vanligt gäller felmarginalerna inte för självselektion och liknande urval som inte har plockats slumpmässigt från en population.

# Lathund:
# 50 % CI = 0.674 z-score
# 80 % CI = 1.282 z-score
# 90 % CI = 1.645 z-score
# 95 % CI = 1.960 z-score
# 98 % CI = 2.326 z-score
# 99 % CI = 2.576 z-score

# Funktion för att räkna ut felmarginal
marginoferror <- function (p, n, z=1.96, population=9600000) {
    if(p>=1) {
      stop("p måste vara proportion under 1, exempelvis 0.60 för 60 %.")
    }
    # Skippa korrektionsfaktorn då den inte ger speciellt mycket
    return (z * sqrt((p * (1 - p)) / n) * 100) # * (1 - (n / population))))
}

# Funktion för att plotta felmarginal vid olika proportioner
plotta <- function (proportion, z=1.96) {
  # Bygg vektor med N och felmarginal
  l <- c(n=0, felmarginal=marginoferror(proportion, 0))
  for (n in 1:2000) {
   l <- rbind(l, c(n=n, felmarginal=marginoferror(proportion, n, z=z)))
  }
  
  # Plotta
  plot(l, type="n",cex.main=1.35, main=paste("Felmarginal vid olika urvalsstorlekar\nnär ett alternativ får ", proportion * 100, "% av rösterna", sep=""),
      xlab="Urvalsstorlek (N)", cex.lab=1.35, ylab="Felmarginal (%)")
  grid()
  points(l, col="red")
  axis(side=1, at=seq(0, 2000, by=500))
  axis(side=2, at=seq(0, 100, by=10))
}

plotta(0.50) # 50 %
plotta(0.50, z=2.576) # 50 % på 99 % CI